2.1 Choice of SAS
The naïve implementation of ray tracing related algorithms iterates through the set of all primitives in the scene and checks ray-primitive intersection for each, which is very time-consuming (linear to the number of primitives) and is a severe bottleneck in performance when the number of primitives gets high. In reality, different spatial acceleration structures (SAS) are applied to solve the problem. They generally improve the speed to logarithmic time and therefore can make interactive ray tracing for complex or even dynamic scene. Octree, BSP (binary space partitioning), BVH (bounding volume hierarchy) and kd-tree are some representatives of the SAS. The SAS generally divide the scene or mesh into recursive sub-spaces which often has a tree-like structure. Among them, octree and BSP are the type of solution which chooses split position in a fixed routine. For example, a typical octree always chooses the center of the space to divide it into 8 sub-spaces. Since they are indiscriminate to the specific geometry that the scene has, they generally exhibit lower efficiency than BVH or kd-tree. BVH or kd-tree, on the other hand, uses some heuristics to determine the partition position based on the specific scene geometry. In terms of the efficiency of BVH and kd-tree, Vinkler et al. (2014) has shown that kd-tree has higher performance for complex scenes than BVH while BVH defeats kd-tree for simple to moderately complex scenes. Considering this, I planned to implement both structures for the freedom of choice with respect to different kinds of scenes. However, due to time limit, I only studied and implemented kd-tree up to now. Therefore, this part will focus on the findings I have on kd-tree.
2.2 Surface Area Heuristics
The construction of kd-tree depends on choosing one dimension and the split position in that dimension in every iteration. A naïve solution is to cycle through the 3 axes and choose the space median every time, giving no better performance than octree. A popular mechanism is Surface Area Heuristics (SAH) (Wald & Havran, 2006), which is based on the greedy algorithm to find a local optimum based on the surface areas of the two child nodes in every step. Instead of finding the global minimum cost which is practically infeasible as number of possible trees grows exponentially with scene complexity, SAH assumes all the primitives in child nodes of a particular step are in leaves, giving the formula of the expected cost of a particular split:
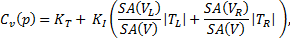
where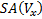 
is the surface area of volume x, 
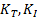correspond to the cost of a traversal step and an intersection step, and 
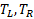are number of primitives in left and right child node. According to probability theory, 
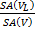gives the chance of uniformly distributed rays hitting the left node which leads to the fact that. This is actually a reasonable assumption as the distribution of rays tends to not follow any certain pattern with the number of ray bounces increasing and geometry of the scene varies. On the other hand, although treating both nodes as leaf overestimates the real cost, the strategy works well in practice (Wald & Havran, 2006). Another advantage of SAH is determination of when to stop splitting is easy, as one can compare the cost of splitting and not splitting directly from the above formula.
In my implementation, I complete the construction of kd-tree on CPU followed by transferring the structure to GPU because construction process involves large data set written to memory and branching are excessively used. Without special optimization and modification to the algorithm, the efficiency on GPU can be much lower than the CPU version. However, Zhou et al. (2008) proposed a clever method of GPU construction of kd-tree which outperforms single core CPU algorithms significantly and is competitive with multi-core CPU algorithms. This potential endows meaning of making GPU construction of kd-tree an issue in the rest of my research.
2.3 Dealing with Pathological Cases
Some pathological cases are often encountered in the construction of kd-tree. The following are illustrated using triangles as primitives. Using a O(N) algorithm which scans through the spatially ordered set of triangle vertices and adds the triangle to the left child when encountering the starting vertex of its bounding box and add it to the right child when encountering the ending vertex, it guarantees if a triangle has any measurable area on left or right side of the split plane, it will exist within that node. However, when a triangle completely lies on the split plane, it will only be added into one of the child nodes (the split position is chosen from the vertices, but it cannot be considered as a candidate whose belonging triangle needs to be added into child node due to unnecessarily extra intersection cost within that node). Since all three vertices have the same coordinates in current dimension (x, y or z), whether the triangle is added into left or right node is arbitrary (Figure 1). However, this causes structural disparity among different child nodes containing the triangle, which further leads to incongruent thread paths as some of the rays directly hit the triangle in front while others may undergo complicated traversal steps to route back from the back side. Nonetheless, a simple solution is to store a marker for every starting and ending triangle vertex indicating whether it is at same position in current dimension with its counterpart. When the split position happens to fall on the specific position of such triangle, the marker is read to determine whether to add it to another child node, which completely solves the problem.
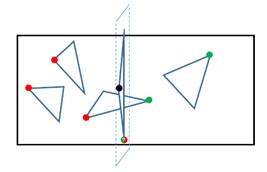
2.4 Kd-tree Traversal
For the traversal of kd-tree, the standard CPU algorithm with stack which stores backside node cannot be directly applied to GPU. First, the stack need to be implemented in fixed length array which guarantees coalesced memory access and reduces memory read and write instead of using linked list or dynamic array implementation of stack. Second, size of the stack item should be compressed as small as possible as complex scene with dozens of kd-tree levels will require the stack to be allocated in local memory instead of the thread registers with very limited capacity. Foley & Sugerman (2005) introduced two stackless traversal algorithms called kd-restart and kd-backtrack. However, without the proper priority information stored for traversal, these algorithms require modification of the traversal path which brings extra time and space complexity: kd-restart directly goes into the nearest leaf and restarts from the root with ray range propelled forward and kd-backtrack stores extra node data to improve traversal restart efficiency as it can restart from a node’s parent. Meanwhile, the worst case of kd-restart degenerates to linear.
A neat solution proposed by Santos et al. (2012) adopted a “short stack” method. Instead of storing 12 bytes as in standard algorithms (4 bytes for node address, 4 bytes for near ray distance (tnear), 4 bytes for far ray distance (tfar)), they discovered that tnear can be derived in the traversal process and it only updates when the traversal finishes checking a leaf, giving an “8-bytes” stack algorithm. The advantage of “8-bytes” stack is not only fewer local memory required, but faster memory access thanks to the fact that an 8-byte load is faster than a 12-byte loads in local memory in CUDA architecture.
By combing a SAH construction of kd-tree and a “short stack” traversal, my SAS has the optimal performance comparing with other combinations. Below is the experiment data of different combinations of construction and traversal methods on different scene (Figure 2). Notice that these data are the result of some SIMD optimization applied to the data structure, which I will discuss and compare the performance with non-optimized ones in part 4.
References
Foley, T., & Sugerman, J. (2005, July). KD-tree acceleration structures for a GPU raytracer. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware (pp. 15-22). ACM.
Santos, A., Teixeira, J. M., Farias, T., Teichrieb, V., & Kelner, J. (2012). Understanding the efficiency of KD-tree ray-traversal techniques over a GPGPU architecture. International Journal of Parallel Programming, 40(3), 331-352.
Wald, I., & Havran, V. (2006, September). On building fast kd-trees for ray tracing, and on doing that in O (N log N). In 2006 IEEE Symposium on Interactive Ray Tracing (pp. 61-69). IEEE.