Yesterday, I saw this intriguing YouTube [video] talking about using a clever trick to solve what was meant to be the hardest problem in 1992 Putnam Math competition.
The problem goes as following: Choosing four random points on the surface of a sphere, what’s the probability that the center of the sphere lies in the tetrahedron spanned by the four points? At first sight, it occurred to me that this was a very difficult multivariate integral problem. However, it turned out that you just need to “flip coins” to get the correct answer.
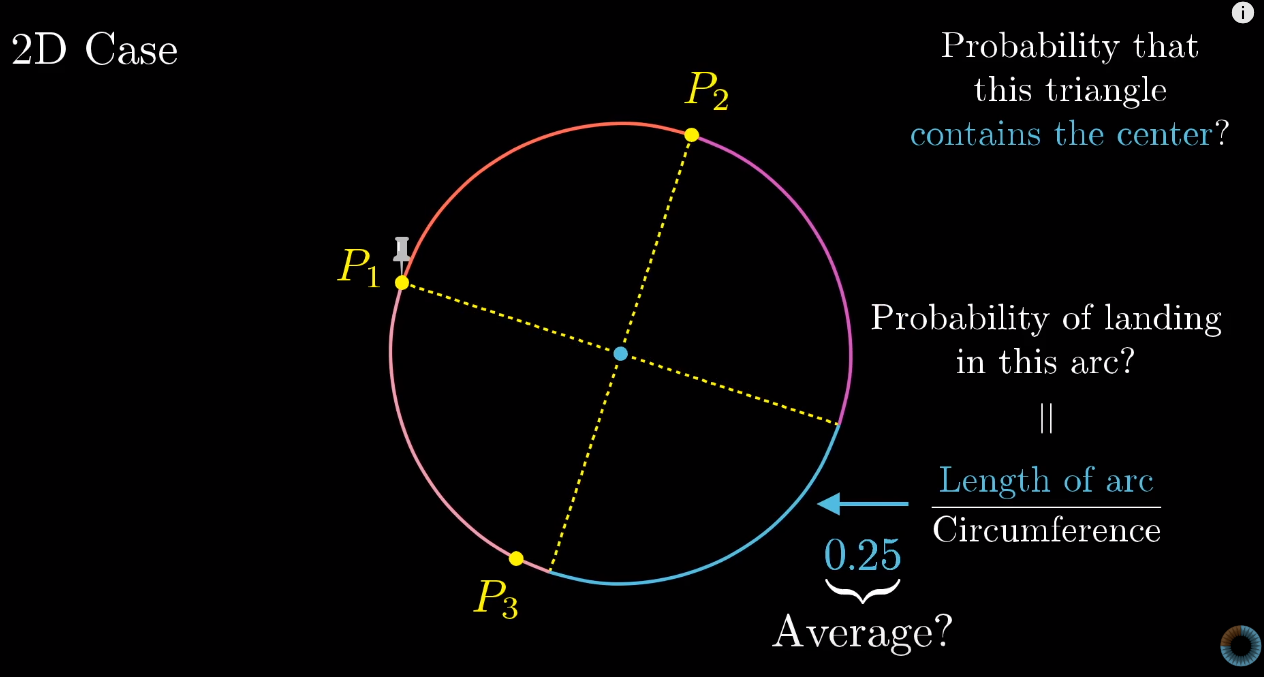
The solution approaches the problem by considering the simplified version first. If there are only three points $P_1$, $P_2$, $P_3$, it’s much easier to consider the case where we fix two points and slide the third point on the circle. Apparently, only when the third point falls on the “opposite” arc (Drawing lines from $P_1$ and $P_2$ through the center, the arc intersected by the lines on the opposite side to that formed by $P_1$ and $P_2$), can the triangle spanned by the three points covers the center of the circle. So given any $P_1$ and $P_2$, the probability that adding a third point $P_3$ forms a triangle that covers the center is the probability that $P_3$ lands on that arc, i.e., the length of the arc over the circumference of the circle since $P_3$ is randomly chosen on the circle. To derive the probability with any $P_1$, $P_2$ and $P_3$ will require $P_1$, $P_2$ to be arbitrarily chosen, which means we can integrate the previous probability over all possible angles between $P_1$ and $P_2$. However, since parameterizing on the central angle is linear, we can directly take the “average length” where the arc formed by $P_1$ and $P_2$ is a quarter circle (we only consider the shorter arc), which gives us a $25\%$ probability.
I believe you are already excited after seeing this 2D case result which was derived without any computation. However, things are getting more nebulous when we go into 3D. We naturally want to extend the 2D reasoning to 3D. Of course, the tetrahedron formed by $P_1$, $P_2$, $P_3$ and $P_4$ covers and only covers the center of the sphere when $P_4$ falls on the circular triangle opposite to the one spanned by $P_1$, $P_2$ and $P_3$. However, getting the “average area” of the circular triangle is non-trivial as it involves evaluating a surface integral with four variables.
So here comes the plot twist, let us go back to the 2D case. Instead of choose three random points, let’s choose two random lines crossing the center of the circle and choose a random point. Each of the random lines represents a point from $P_1$ and $P_2$ and $P_1$ and $P_2$ can be on either end of their underlying line, at equal probability. This should be equivalent to the case of choosing three random points. Since there are only 4 different combinations of $P_1$ and $P_2$ lying on a specific end of their corresponding lines and only one of these combinations yields $P_1, P_2$ to be on the opposite side of the circle as the randomly chosen $P_3$ (in other words, not all of them are on the same semicircle), we have a one-fourth chance of forming a center-covering triangle. It is very similar to flipping two coins - one specific coin must be head and the other one must be tail, which has a $1/4$ probability.
And what’s awesome about this reasoning is that it extends seamlessly to the 3D case. Four random points just become three random lines crossing the sphere center and one random point. This time, we are flipping 3 coins to generate all possible combinations and only one out of all 8 cases gives us the situation when the fourth point is on the opposite side of the sphere as the other three points. So the probability that four randomly chosen points on a sphere covers the center of the sphere is $1/8$.
This was such an elegant proof and the reasoning process was very inspiring. In most often cases, you can go to simpler cases first (in this case, going down one dimension and fixing some points) before solving a hard problem. More complex cases are usually generalization or combination of simpler cases, the essence of the problem should be the same. Therefore, considering the simpler cases makes you more likely to grasp the essence of the problem (but we need to beware of the false positives when generalizing reasonings) rather than being overwhelmed by the harder problem. A joke probably from the Institute for Advanced Study (Einstein, Godel, von Neumann, Yang Chen-Ning, etc. have worked there…), there were signs at the balconies of the buildings saying “before you jump, have you ever considered dimension one?”. Another more important insight from this video is that, changing the formalization can be the plot twist of solving a hard problem. This happens when the solver of the problem found that generalizing the 2D result to 3D was very hard and went back to 2D. In more philosophical words, it is actually the language, whether it is text or graph, that defines the way we think. The essence of the problem is the “thing” itself but some languages might do a better job than others describing it. In this case, four random points and three random lines plus one random point are just two different languages describing the same thing. However, one language is a better tool to approach the essence of the problem than the other. And we are less likely to discover that language if we don’t go to the low dimension case. Although it is very subtle, we can always practice the idea by thinking in different angles and formalize the problem is multiple different ways.
Up to now, the solution is only described in a very intuitive way so we can say we have the idea of the proof but not the proof itself. To formalize the proof, some mathematical tools need to be used. An [article] here gives a formal proof by expressing the points as position vectors with the sphere center being the origin, and by requiring the origin to be expressed as a convex combination of the four position vectors, i.e. all weights having the positive sign, matching the only case out of 8 possible cases. This article also generalized the problem and derived some interesting facts. Obviously, the easiest generalization is $n+1$ points on a $\mathbb{R}^n$ dimensional ball, which gives a probability of covering the center of $\frac{1}{2^n}$.
References
3Blue1Brown(Grant Sanderson). “The Hardest Problem on the Hardest Test.” YouTube, 8 Dec. 2017, www.youtube.com/watch?v=OkmNXy7er84. (All images in this article are captured from the video. The article also heavily used the ideas in the video.)
Howard, R., & Sisson, P. (1996). Capturing the origin with random points: Generalizations of a Putnam problem. The College Mathematics Journal, 27(3), 186-192.
Kedlaya, K. S., Kedlaya, K. S., Poonen, B., & Vakil, R. (2002). The William Lowell Putnam mathematical competition 1985-2000: problems, solutions and commentary. MAA. Retrived from https://www.amazon.com/William-Mathematical-Competition-1985-2000-Problem/dp/0883858274 (The covered of this book is used as the header image of this article.)