Abstract
Interpolation is a core operation that has widespread use in computer graphics. Though higher-order interpolation provides better quality, linear interpolation is often preferred due to its simplicity, performance, and hardware support.
We present a unified refactoring of quadratic and cubic interpolations as standard linear interpolation plus linear interpolations of higher-order terms and show how they can be applied to regular grids and (triangular/tetrahedral) simplexes Our formulations can provide significant reduction in computation cost, as compared to typical higher-order interpolations and prior approaches that utilize existing hardware linear interpolation support to achieve higher-order interpolation. In addition, our formulation allows approximating the results by dynamically skipping some higher order terms with low weights for further savings in both computation and storage. Thus, higher-order interpolation can be performed adaptively, as needed.
We also describe how relatively minor modifications to existing GPU hardware could provide hardware support for quadratic and cubic interpolations using our approach for both texture filtering operations and barycentric interpolation.
We present a variety of examples using triangular, rectangular, tetrahedral, and cuboidal interpolations, showing the effectiveness of our higher-order interpolations in different applications.
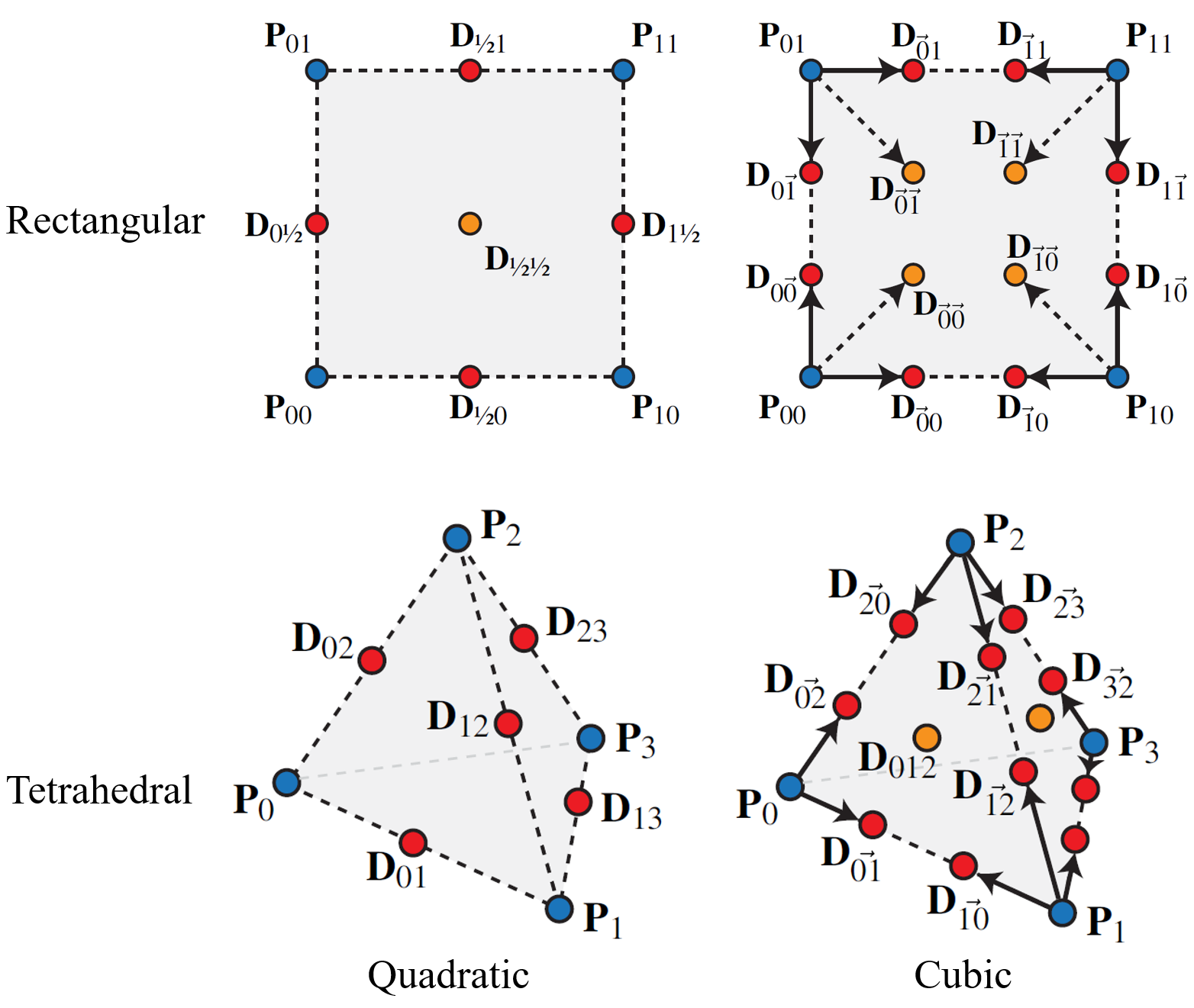
We express quadratic and cubic interpolation as standard linear interpolation (using blue data points) plus linear interpolations of high order difference terms (“D-terms”, red and orange data points). The figure shows the rectangular case that builds high order interpolation on top of bilinear interpolation and the tetrahedral cases that builds on top of linear barycentric interpolation. The orange data points account for the highest order terms in the corresponding high order polynomial and can be usually omitted without affecting the interpolation quality.
Our formulation provides savings of hardware bilinear operations (with proposed hardware modification) compared to the standard technique. Furthermore, we allow setting a threshold to discard high order difference terms (“D-terms”) to save more computations. This figure shows that our adaptive hardware cubic interpolation uses only 39% more bilinear operations than standard bilinear interpolation in the task of temporal history lookup in temporal antialiasing. We avoid the common resampling blur of bilinear interpolation with a cost similar to bilinear interpolation.
BibTeX
@article{Lin2021,
author = {Daqi Lin and Larry Seiler and Cem Yuksel},
title = {Hardware Adaptive High-Order Interpolation for Real-Time Graphics},
journal = {Computer Graphics Forum (Proceedings of HPG 2021)},
year = {2021},
volume = {40},
number = {8},
numpages = {16}
}