This series introduces you to the implementation of physically based rendering in light-weight game engines by GLSL shaders and precomputed textures. With our techniques, most phsically based surface-to-surface reflection can be simulated across a variety of material ranging from metals to dielectrics in HDR lighting and subsurface scattering can be simulated as well with human skin as an example, so that you can achieve high fidelity of game objects with fewest resources. Most of the contents are collected from my project report as an intern R&D engineer in a game company from May to Nov 2015. I want to share what I learned of, what I thought about and what I have done in this topic so that it makes easier for more people trying to dig into this topic. There are 6 episodes.
- 1 Introduction to PBR
- 2 Image Based Lighting
- 3 Subsurface Scattering – Human Skin as Example
- 4 High Dynamic Range Imaging and PBR
- 5 Real-time Skin Translucency
- 6 Improvement of PBR
1.1 Photorealistic Rendering and Shading Language
Photorealistic rendering is one crucial part of computer graphics. In early days of computer graphics, most hardware only supports fixed function rendering pipeline due to performance limitation. Things like lighting and texture mapping were processed in a hard-coded manner, resulting in coarse and unrealistic images. Nowadays, with the development of hardware power and software techniques, rendering pipelines have become programmable. High-level shading languages with unlimited possibilities of rendering effects are directly applied in specific stages of rendering pipelines. Many ideal physical models have been successfully implemented with GPU programming to render highly photorealistic 3D scenes and characters.
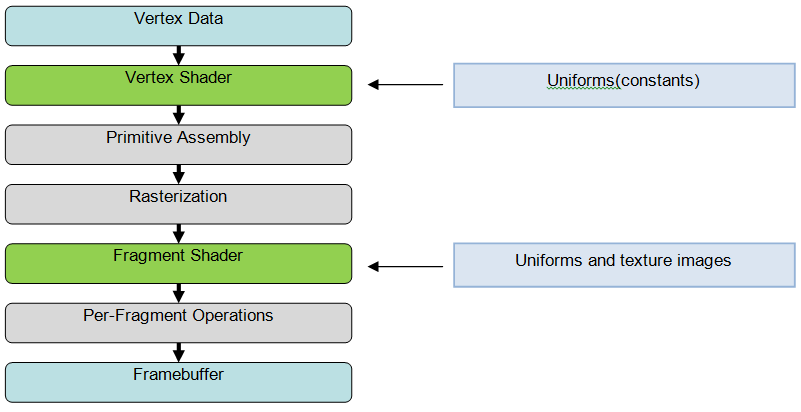
One of the most common high-level shading language is OpenGL Shading Language (GLSL), which is also the main tool used in this project. Unlike stand-alone applications, GLSL shaders require an application that calls OpenGL API and are passed as a set of strings to graphic driver for compilation. There are two kinds of most commonly used shader, the vertex shader and the fragment shader, which are applied to each mesh vertex and each fragment (i.e. covered pixel) respectively in the graphic pipeline. The vertex shader determines the final position of mesh vertices that are presented to user. It also passes variables that relate to normal, color or coordinates to fragment shader. The fragment shader is then executed to give each covered pixel an intended color. In addition, external uniforms can be passed into the shaders to provide material like texture sample and camera position.
Here is a simplified diagram showing where shaders are applied in the graphics pipeline:
1.2 Implementation Based on Blender Game Engine
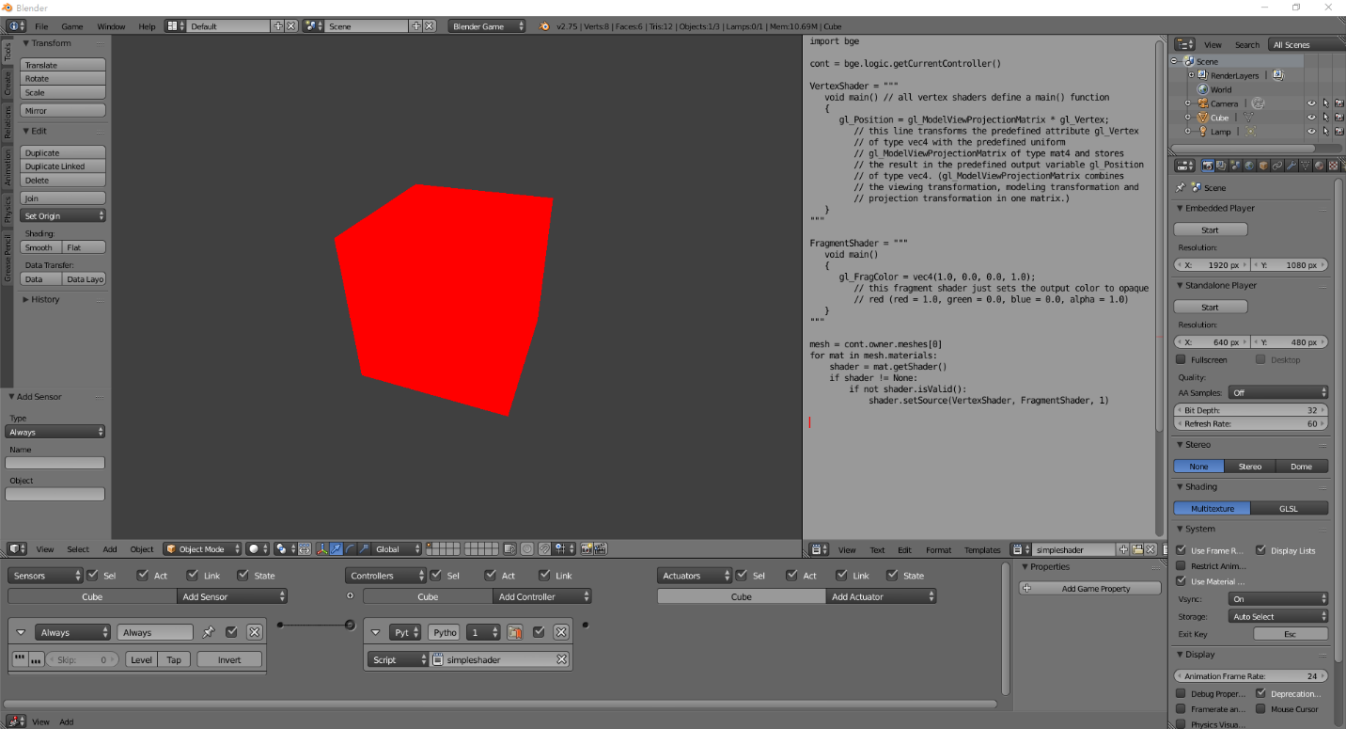
In this series, we mainly use Blender as the example of light-weight game engine and the platform for graphic rendering and 3D games implementation. As a professional open-source 3D computer graphics software, Blender supports many functions including 3D modelling, UV unwrapping, texturing and rendering. Using OpenGL as its graphic library, Blender supports customized GLSL shaders in rendering in its Blender Game Engine. Figure 2 is a screen capture from Blender 2.75 showing the effect of a simplistic shader that shades a cube with purely red color with no lighting. It is noticeable that the shaders are passed as arguments of Blender’s Python API, which are then passed to the internal OpenGL API. Like other game engines, Blender also supports passing game primitives like material’s lighting configurations and camera’s view transformation matrix to the shaders, which allows intuitive coordination between shaders and the scene.
1.3 Physically Based Rendering
Physically based rendering (PBR) is a growing trend in CG game and film industry. Basically, PBR is rendering images according to math model of real-life physics. Thanks to the growth of computation power, many complex models can be approximated in high precisions currently, which gives highly realistic images.
A very important issue in PBR is to simulate realistic lighting effect, in which bidirectional reflectance distribution function (BRDF) is used. A BRDF gives the relationship between irradiance and radiance, i.e. how light intensities distribute in each reflection direction after a light ray hit an opaque surface in given angle – which includes all kinds of reflection (e.g. specular reflection and diffuse reflection), depending on the material of the surface. Usually, different BRDFs that assumes specific properties of the surface are combined to give realistic lighting result. Common BRDFs includes Lambertian model (assuming surface to be perfectly diffuse), Blinn-Phong Model (a traditional lighting model that approximates both diffuse and specular reflection) and Cook-Torrance model (a more complex model that treats surface as microfacets to give more accurate specular reflectance with Fresnel effects).
The use of complex textures for different physical attributes is a crucial factor that makes PBR realistic. When it comes to complex models that has different physical attributes in different part of surface, a very important constraint must be considered – conservation of energy. In other words, the more reflectivity (short for specular reflection) an object exhibits, the less diffusion (short for diffuse reflection) it gives. Metalness is a parameter used to determine the ratio between reflectivity and diffusion (which sum up to 1). The reason of the name is that metal usually has a high reflectivity and low diffusion and dielectric (non-metal) material has the reverse condition. Therefore, metalness map can be used as a texture to determine the metalness in different parts of the object (most real-life object has different metalness across its surface), which grants artists’ power. Another attribute that has to obey energy conservation is roughness. Treating any surface as infinite many microfacets, being rougher is only about having a larger variance of microfacet orientation, which obvious obeys energy of conservation – the rougher a surface is, the larger the reflected image spreads. Similarly, another texture – roughness map can be used here.
Direct illumination from simplified light models is easy to implement in shaders. Choosing a suitable BRDF and knowing related material attributes is enough to give a result. However, when it comes to global illumination, calculating the correct lighting becomes not so trivial. In most scenes, the background environment reflects light and illuminates its surroundings indirectly. Also, realistic lights may have different shapes and color distribution. These phenomena exceed the capability and constraints of light models by far. Although BRDF is also applicable to these situations, it requires integral and other complex mathematical computations that cannot be carried out directly. Therefore, a technique called image based lighting (IBL) comes to rescue, which is also the first issue that I come to research and implement. In next episode, I will talk about how I implement the image based lighting.
Another issue is subsurface scattering. BRDF assumes an opaque object surface, in which reflections all happens at the incident point (the diffuse reflection is actually scattered light due to material’s internal microscopic irregularities, and can be treated as directly happening at the surface). However, for materials that are not so opaque (for example, human skin), the effect of transmittance and subsurface scattering cannot be ignored. Calculating transmittance is easy as it is actually an inverted BRDF on the opposite side of the surface. However, surface scattering is relatively complex, as the lights reflected from subsurface can exit at another location other than the point of incidence. There is also a general function called Bidirectional Surface Scattering Reflection Distribution Function (BSSRDF) that describes the relation between the irradiance and radiance in this phenomenon. However, the function is too general and special case may be taken to handle specific tasks, in order to be more computationally efficient. Since my task is currently restricted to the rendering of human skin, I will focus on the special case of subsurface scattering happening inside human skin. Episode 3 will introduce the method I use and the detail of implementation.
List of Figures
Figure 1: Rendering Pipeline. Source: My original diagram created by Word
Figure 2: A Sample Shader in Blender. Source: My original screenshot of Blender