3.1 Subsurface Scattering and Fidelity
So far, our PBR model only considers the interaction of light at the surface of an object. This is not a problem as many models in 3D games is nearly opaque. However, when it comes to objects with a certain level of depth and translucency, like skin, marble, leaves and wax, the effect of subsurface scattering cannot be neglected if we want to get realistic results. Subsurface scattering often has an effect to make the overall lighting softer as light at a position seems to be overflowing to its neighboring areas.
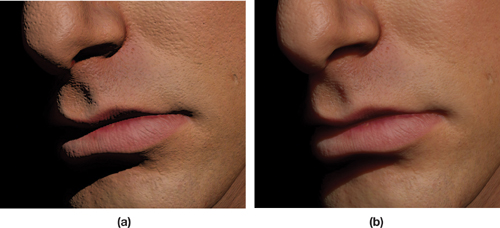
Among all kinds of materials that requires subsurface scattering, human skin is relatively complex. Human skin has numerous layers and realistic rendering requires a model of at least 3 layers (the thin oily layer, the epidermis and dermis) (d’Eon & Luebke, 2007). The first layer contributes to the specular reflection effect which can be simulated by Cook-Torrance Model. The other two layers requires the task of subsurface scattering. This kind of multi-layer subsurface scattering has an important meaning for research. The pictures below shows the comparison between rendering without (a) and with (b) subsurface scattering. The result without subsurface scattering appears very dry-looking and unrealistic, while the latter one seems natural (Figure 8).
Many games include highly detailed human models. Complex textures including bump map has been applied to simulate the human skin. To match with that level of fidelity, subsurface scattering is a must-do.
3.2 Diffuse Profile and Gaussian Approximation
As mentioned before, in subsurface scattering, the relationship between the irradiance and radiance is governed by BSSRDF. As the skin is highly scattering, a function called dipole diffusion function has been introduced (Jensen et al., 2001) to give efficient simulation of this situation. The BSSRDF is reduced to rely only on the material’s scattering properties, the Fresnel terms at point of incidence and point that radiance comes out, and the distance between the two points.
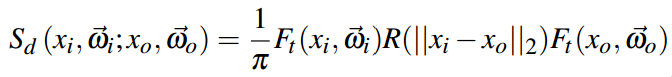
In the formula above, S represents BSSRDF, Ft stands for Fresnel transmittance and R is the material’s diffusion profile.
The diffusion theory is later extended to simulate scattering effect in multiple-layer material by the use of multipole (Donner & Jensen, 2006), to support more realistic rendering. The advantage of diffusion profile is that it is an empirically determined function. One only needs to do experiment on specific material to get a numerical form of the function and draw the shape of the function. The dipole or multipole is then used to give an analytical approximation. However, the computation of such functions is very complex. Luckily, d’Eon et al. invented an approximation method (2007). They fit the curve of multipole by using weighted sum of multiple Gaussian functions with some heuristic coefficients.
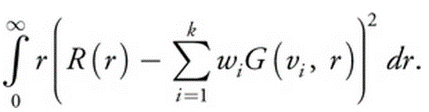
Certain coefficients are chosen, such that the error represents by the formula above is minimized. For skin, six Gaussians are required to match the three-layer diffusion profile accurately. The coefficients for each Gaussian are determined respectively for red, green and blue channel.
3.3 Texture-Space Diffusion vs. Pre-Integration
With the present of skin diffusion profiles, many methods can be chosen to compute the subsurface scattering. A popular method invented by Borshukov and Lewis is called texture-space diffusion (2005). The idea is storing incident lights in texture space and uses convolution steps to simulate diffusion, which is similar to the pre-filtered environment map in IBL. However, human characters in games are likely to moving frequently and changing of diffusion texture is inevitable, which implies real-time rendering to texture (RTT). Blender, as my working platform, does not have a customized texture buffer. In order to avoid editing Blender’s source code, I chose to find another method that does not use RTT.
Penner and Borshukov introduced an approximation method by pre-integrating the subsurface scattering effect in skin (2011). In this method, shading process becomes local; the calculation is reduced to a simple pixel shader - no extra rendering passes are required. The idea is that the visible scattering effect can be considered as a composite result of mesh curvature change, normal map bumps and shadows.
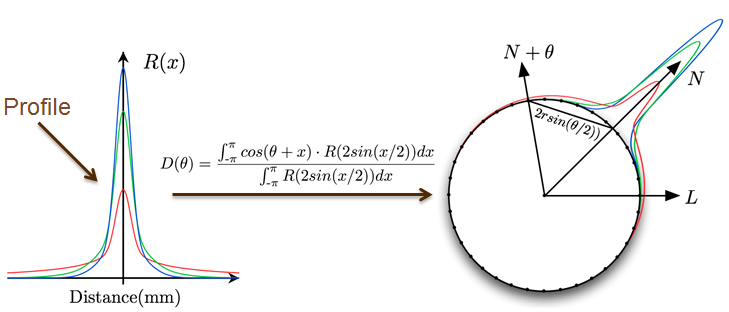
The first term, change of mesh curvature, affects incident light (and thus scattering) together with the angle between light direction and normal direction (described by N∙L). A 2D LUT using the curvature and N∙L can be calculated representing accumulated light at each outgoing direction as a result of lighting a spherical surface of a given curvature, which approximates a spherical integration in BSSRDF with a ring integration. Of course, skin diffusion profiles are used in the computation.
When using a normal map as bumping texture, since the effect of scattering light coming from a bump appears very similar to reflecting light from a surface with no scattering and blurred out bumps, the scattering effect can be approximated by blurred the normal map. The level of blurring is different for each color channel, because different wavelength has different diffusion profiles. Using a normal map for scattering without blurring it for each color channel in different degrees would result in an unnatural grainy shading.
In my implementation of this pre-integration method, the influence of shadows is temporarily omitted since currently I have not found the method to add a real-time shadow when customized shaders are used in Blender Game Engine. This issue will be tackled later. The combination of ring integration and blurry normal map already gives a nice result, if we ignored the shadow
The ring integration texture was generated in C++ with the aid of OpenCV. 1024 samples were taken for each independent variable combination from –PI/2 to PI/2 to ensure accuracy.
Another point worth to mention is that GLSL has a built-in function in its fragment shader to help calculating the curvature. Although it offers relief for programmers, it is computed in the basis of triangle orientation and thus curvature is uniform inside a mesh triangle. For low-poly meshes it becomes a problem as the edge of triangles at positions with strong scattering effect would be very obvious. To alleviate this problem, I stored the curvature in a texture and read from it in vertex shader. The vertex colors would then be interpolated across each triangle like what happens in Gouraud shading.
Indirect light sources can also be used for subsurface scattering. The combination of image based lighting with pre-integration scattering gives more vivid rendering results.
References
Borshukov, G., & Lewis, J. P. (2005, July). Realistic human face rendering for the matrix reloaded. In ACM Siggraph 2005 Courses (p. 13). ACM.
d’Eon, E., & Luebke, D. (2007). Advanced techniques for realistic real-time skin rendering. GPU Gems, 3, 293-347.
Donner, C., & Jensen, H. W. (2005). Light diffusion in multi-layered translucent materials. ACM Transactions on Graphics (TOG), 24(3), 1032-1039.
Jensen, H. W., Marschner, S. R., Levoy, M., & Hanrahan, P. (2001, August). A practical model for subsurface light transport. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques(pp. 511-518). ACM.
Penner, E., & Borshukov, G. (2011). Pre-integrated skin shading. Gpu Pro,2, 41-54
List of Figures
Figure 8: Comparison Between Skin Rendering Without and With Surface Scattering. Source: GPU Gem 3 online book on http://http.developer.nvidia.com/GPUGems3/gpugems3_ch14.html
Figure 9: Dipole Diffusion Function. Source: online document of d’Eon et al on http://www.eugenedeon.com/wp-content/uploads/2014/04/efficientskin.pdf
Figure 10: Error of Gaussian Approximation. Source: Same as Figure 9.
Figure 11: Illustration of Diffuse Scattering Integration on Ring. Source: Penner’s slides at SIGGRAPH 2011 Courses on http://advances.realtimerendering.com/s2011/Penner%20-%20Pre-Integrated%20Skin%20Rendering%20(Siggraph%202011%20Advances%20in%20Real-Time%20Rendering%20Course).pptx