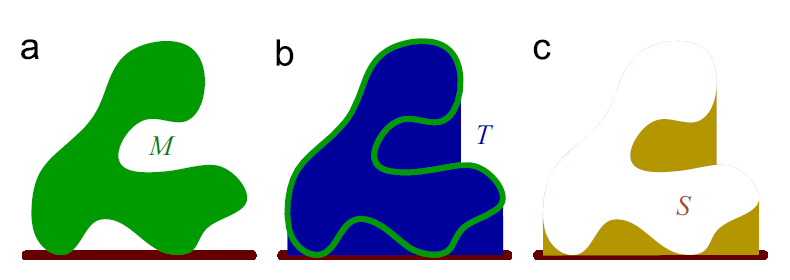
This post shares a very interesting topic I learned in my internship at Graphics Lab, Xiamen University, during last summer. Due to the fact that 3D printing is additive manufacturing, upper layers need to be glued upon lower layers, thus creating a very strict constraint that we can only print a layer within the boundary of its lower layer (but in practice, some material has some inner cohesion that allows some part of the layer protrudes from the supporting structure).
To solve this issue, people have been using a different kind of material as the complementary supporting structure - when we print a layer, we also print the additional region that the upper layer projects to, using a different material, which can be dissolved using some organic dissolvent like limonene, separating the model from the supporting structure.
A illustration of how support material is dissolved.
(source: https://3dprintingindustry.com/news/upon-kickstarter-funding-helix-3d-printer-announces-stretch-goals-20377/)
So here comes the interesting question, how are we going to adjust the orientation of printing such that the volume of the supporting structure is minimized? A minimized supporting volume also minimizes the cost on material. Imagine we need to replicate a dinosaur - that would be a huge saving on material! A naive answer is, go over all possible orientations. For each orientation, slice the model vertically into layers with the printing resolution. Starting from the top layer - for each layer, if the current pixel (corresponding to the printing resolution) is a hovering pixel, we increase the counter by the number of slices required to reach another piece of solid that lays below. Then the support volume is proportional to the number in our counter. However, it would require O(M*N^3) steps (which is often the case when the hollow in the mesh is extremely scattered), where M is number of orientations we choose! To obtain a coarse estimation, usually we will use the combination of azimuth and altitude angles (yaw and pitch) corresponding to the orientation of segments we used to create a sphere mesh (32x32, for example). Take the resolution of common 3D printer - 250 DPI - for example, for a small 1x1x1 inch object, the number of steps is in the order of magnitude of 10 billion, which is quite expensive!
A cleverer way is to realize that we can find the analytical solution of the volume of mesh by summing up the signed volumes formed by the origin (arbitrarily chosen) and all oriented faces. Since a properly prepared mesh should have consistent winding of vertices on each face, the signed volumes computed from the triple scalar products of the position vectors of three ordered vertices on all faces should sum up to get the volume of the mesh. In the case where the origin is inside the mesh, all signed volumes should be positive. If the origin is outside the mesh, there will be some part of the positive volumes of back-facing triangles compensating for the negative volumes of front-facing triangles. Also, the sum of the triple scalar products should be multiplied by one sixth, since that is the portion a tetrahedron takes from the parallelepiped. Here’s a graph to help you understand it.
Illustration of how to calculate the mesh volume by adding signed face volumes.
(source: https://n-e-r-v-o-u-s.com/blog/?p=4415)
The next step of this method is, instead of scanning through all empty voxels, you only look at the uppermost contour and find the difference between the height with the ground (determined by lowest point of the mesh in current orientation), which could potentially reduce the complexity to O(MN^2), using proper implementation. Then as you could’ve imagine, this volume - the supporting volume of highest contour, minus the volume of the mesh, should give us the volume of the support structure. But if we want to implement this by voxelizing the mesh, we still get a O(MN^3) complexity.
The method propsed by the authors. (source: graph in the authors' paper)
Actually, we can do this without voxelization. The solution is proposed by Massarwi et al. in their 2015 paper Orientation Analysis of 3D Objects Toward Minimal Support Volume in 3D–printing. Since we have the mesh representation, why don’t we just place a orthographic camera on the top of the mesh and rasterize it to the screen? The z-buffer can then be used to calculate the height of the element on the topmost contour. This is the kind of task that GPU is designed for and very efficient at. In high-end graphic cards, we can have 60 fps with a scene that contains over 100k triangles with all kinds of VFX. Therefore, it should be lightening fast to calculate support volume for an specific orientation. However, we need to determine the clipping planes of the orthographic camera, the distance between which is the depth range (used for scaling the z value) the mesh spans in current orientation. To achieve this, we still need to do some vector multiplication for each vertex to see its z value transformed from the model space, which takes much longer time than rasterizing. In other words, it becomes the bottleneck.
The original paper doesn’t specify how to do the depth range calculation. A proper way to reduce the time is to use GPU parallelization like CUDA, OpenCL, or just compute shader. The case of finding the lowest point would trivially translate to mapping each model space vertex to the transformed z value and use parallel reduction to find the minimum, both of which can be achieved by simply calling Thrust API, without the need of writing CUDA kernels.
After eliminating this bottleneck, we can consider reducing the cost of the rendering depth buffer. Since depth buffer is produced by fixed function pipeline, the only optimization we can do is probably to enable early fragment test. However, instead of rendering a single orientation at a time, we can process all orientations together. For the rasterization stage, we can use OpenGL’s multiple layer rendering feature to put all orientations into one texture (OpenGL 4.5 requires the number of layer to be at least 2048, leaving enough slots for 1024 orientations). We simply need to add a geometry shader that dispense one triangle to different layers using parallel invocations and a loop within each invocation. It turns out that we can gain an overall 40% speedup.
Using the above optimizations, we have a much more efficient workflow to find a coarse estimation of the orientation that yields the minimum support volume. It now reduces to the problem to find the accurate (in the available precision, of course) solution. The authors in the paper used a mixture of analytical and numerical method. They realized that the function of support volume of the mesh is piece-wise smooth, where any orientation that contains a face that is perpendicular to the ground yields a non-differentiable point on the function. However, these non-differentiable points can be analytically determined. Although such points can be very dense, we are only looking at a small region determined by our coarse estimation. The authors use a derivative-free numerical optimization method (Lucidi & Sciandrone, 2002) to perform minima searching at each smooth region, where there is a need to sample the function, the rasterization pipeline is called (a math function can be any computational process!).
The optimization process is sort of similar to gradient descent performed in every smooth region. Therefore, we can still parallelize by the smooth regions. However, it turns out that using CPU multiprocessing (Intel TBB) is much faster than using CUDA, probably because the optimization process is very logically intensive and has many branches. Of course, we could develop some new methods that makes the algorithm more suitable for GPU. Due to time limit, this more complex problem is listed as a future attempt.
Also, apart from what I’ve implemented, I also suggested a possibility of using bounding boxes to accelerate the finding of the lowest point in coarse optimization. The original method searches through all mesh vertices to find the minimum, which wastes the locality of the lowest point. If we use a BVH for the mesh, we can (physically) rotate the BVH and exclude all nodes whose bounding boxes lie completely above the bounding box that contains the lowest point in last search. In this way, we only need to look at vertices in a few bounding boxes, which can significantly speed up the computation.
Overall, it is a fun journey to optimize an algorithm for optimization problem, especially for this task - finding the minimal support volume for 3D printing - which is both useful and conceptually simple.
References
Ezair, B., Massarwi, F., & Elber, G. (2015). Orientation analysis of 3D objects toward minimal support volume in 3D-printing. Computers & Graphics, 51, 117-124.
Lucidi, S., & Sciandrone, M. (2002). A derivative-free algorithm for bound constrained optimization. Computational Optimization and applications, 21(2), 119-142.