Now we’ve added BVH as an alternative choice of SAS! It is necessary for real-time ray tracing against dynamic scene geometry with complex moving meshes as it maintains the interior hierarchy of the mesh and only updates exterior hierarchy which is usually much simpler to do.
8.1 Triangle Clipping in Kd-Tree Construction
An important issue in kd-tree construction is the necessity to clip
triangles which span across the splitting plane in each level for
accelerating intersection. In their 2006’s paper, Wald & Havran
suggested that on average, for a kd-node with N triangles, there are
O(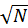
) triangles spanning across a splitting
plane. Normally, we check whether the ends on current chosen splitting
axis of the triangle’s bounding box are in distinct sides of the
splitting plane to determine whether to add it in both of the child
nodes. However, it may be the case that the triangle does not overlap
one of the child node, even though in one dimension it does. Such error
will be accumulated to a situation that the whole triangle lies outside
of its node’s bounding box. With the increase of kd-tree level,
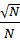will be increasingly close to 1, which
means at leaf level, one would expect many false positives to occur in
intersection test, unnecessarily increasing the time for intersection.
In addition, adding spanning triangles to both sides unnecessarily
increases the workload of construction as one has to test the vertices
against the boundary of the bounding box in current kd-tree level to
avoid choosing a splitting plane outside the bounding box.
Since it is convincing from the analysis above that clipping triangle does has an obvious boost on intersection performance, which is often a bottleneck for path tracing, we offer some test cases to quantize the rate of performance improvement. After that, we will explain how to clip the triangles, which is a relatively simple task without the need of importing third-party libraries.
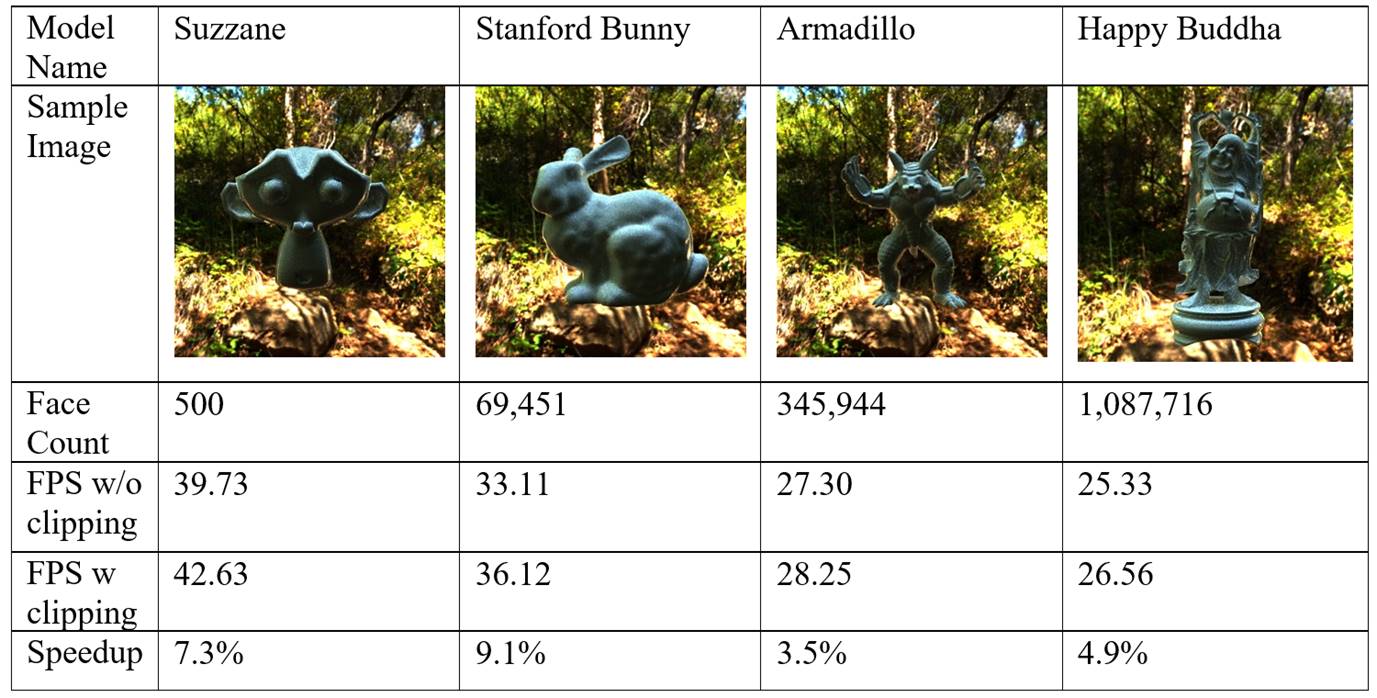
From the table, we can observe that clipping triangles results in a speedup from 3.5% to 9.1% for different mesh complexity, which is not very drastic but obvious enough to confirm the effect of triangle clipping.
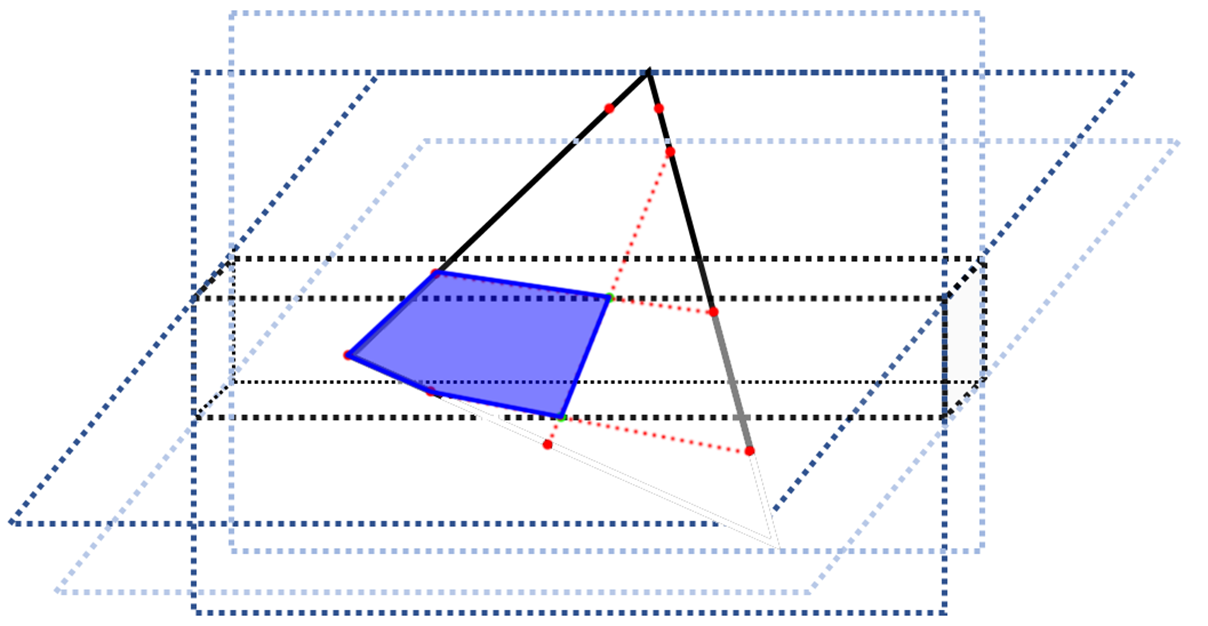
We will now illustrate how to clip arbitrary triangle against box with an example where a triangle is clipped to a pentagon. In Figure 2 below, we determine the intersection between any pair of vertices that lies in different sides of each of the 6 faces of the cuboid. Then, in the plane spanned by each of the 6 faces, we calculate the intersections the line extended by the two intersection points (if there is two), which may be zero, one or two in number. Any intersection will become a vertex of the clipped polygon. If the end vertex itself lies inside or on the border of the box’s face, it also become a vertex of the clipped polygon. Notice that the process is trivially parallelizable for the 6 faces, except for the memory write, i.e. expanding current bounding box to contain the new vertex. If the construction is running on GPU, parallelizing on 6 faces can decrease considerable amount of time for the clipping stage in each level, which does not process too many triangles and is solely occupying the GPU.
8.2 SAH-based BVH
As mentioned before, BVH is a crucial component for real-time ray tracing against dynamic scene geometry. Similar to kd-tree, the probabilistic analysis applies to the decision of splitting plane in each tree level, which naturally leads to the fact that greedy choice of local optimum gives the best available algorithm for optimizing traversal cost. The only difference between kd-tree and BVH in terms of surface area heuristic is – BVH is a hierarchy of objects and kd-tree is a hierarchy of subspaces. Therefore, refitting bounding box is necessary when dividing the node into child nodes, which turns out to be a time-consuming bottleneck in construction.
Unlike kd-tree construction which uses a dynamic array or vector to store all triangle events, BVH construction needs to maintain a binary search tree for each dimension. The shrinking side of the refitting process requires us to search and delete the events that are recently switched to the expanding side and add them to the BST of that side. Initialization of the BSTs costs O (N log N). Each check of splitting position costs O(log N) and the whole process of best plane determination costs O (N log N), leading to a O (N log N) total time complexity. Even worse, maintaining binary search tree for three dimensions implies a big constant of 3. For this reason, the construction of SAH-based BVH often causes serious overhead latency in complex cases. Fortunately, a simplification method which equally divides the space into a small number of buckets was proposed by Pharr & Humphreys (2011) in their famous Physically Based Rendering book. Partitions are then only considered at bucket boundaries, which gives much more efficient construction while remaining as effective in traversal as the original method. It is easy to figure out that the whole construction only requires O(N log N) time since bucket number is a constant. Meanwhile, a binned partition implies easier and more efficient parallelization on GPU. Due to time limit, a GPU construction for BVH is not implemented, as there exist well known parallel binned BVH construction methods.
The traversal of BVH is easier to implement than kd-tree but less efficient in performance. Since we cannot guarantee any deterministic spatial order of BVH nodes as they may overlap each other in any form, we cannot terminate traversal after we find a hit in leaf. Although the child nodes of a BVH node are also stored in a “front-back” order. It only indicates the spatial order of the centroid of two bounding boxes as in construction the decision of affiliation of triangle is based on the side of its centroid. It is entirely possible that the “back” BVH node contains a nearer hit than the “front” node. Nevertheless, such probability is not high. In most cases, the “back” BVH node will not have any intersection in the trimmed range after intersection is done for the “front” BVH node, after which it will be popped from stack. If then the stack is checked to be empty, the function returns the nearest intersection if there is any.
8.3 Automatic BVH Refitting
A simple solution of tracing dynamic scene geometry is to recursively refit the local BVH whenever intended object moves beyond its parent’s bounding box. If tree levels outside the intended object is much less than tree levels inside or movements of the object is spatially limited, such method has a very low time cost. Attention must be paid to the fact that shrinking refitting is also necessary when object moves towards the original position, for which we can store a record of the moving direction of current frame as bitmask of 3 axes. If the bounding box of moving object in last frame borders its parent or ancestor with respect to any of the current dimension of moving read from the bitmask, we perform a shrinking refit. Also, for every movable object, a translation vector is stored to be used as an offset in triangle intersection. However, when assumption of less exterior tree level does not hold or there is violent movement of objects, we need to consider alternative methods other than the purely refitting. A combination of splitting, merging and rotation operations can be performed on tree structure (Kopta et al., 2012), which massively increases the rendering speed for complex animated scenes as it avoids structural degeneration in naïve refitting.
However, such method also has its limitation. When most of the objects in the scene are animated (e.g. particle system), update of BVH is serialized due to necessary atomic operations for many threads changing the boundaries of the same bounding box. In this situation, it is better to rebuild the BVH rather than modify it.